Results
Below are summaries of our final model results, for more information please read our detailed report linked here: https://github.com/edinhluo/DSC180-Capstone-Project/blob/main/report.pdf
Non-Adaptive and Adaptive Pooling
Using the same parameters as Two Step Adaptive Pooling (2-STAP)[3] with a sample size of 961 sample size, 52 tests, and 5 infected samples, our nonadaptive pooling algorithm had an average accuracy of 97.02% for a pool size of 192.
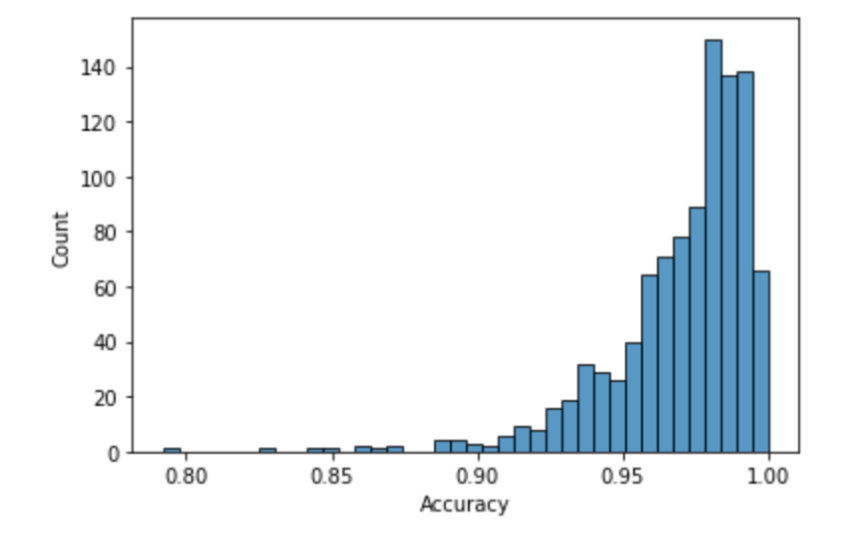
We ran our first adaptive algorithm (running initial tests, ruling out negative indexes, and pooling from the remaining indexes) with 70 max tests and 10 infected, while varying population and the simulation showed similar accuracies to the non-adaptive pooling scheme. The adaptive algorithm performs better at smaller population sizes, but has relatively similar accuracies with the nonadaptive strategy as the population size increases.
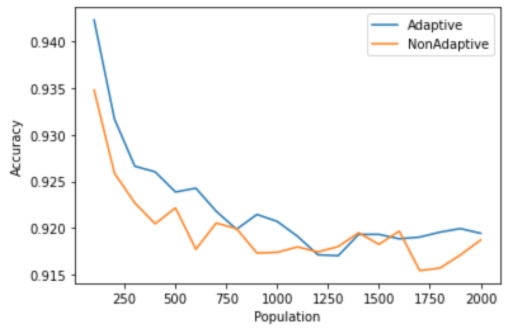
Disjoint Pooling and Limited Pool Size
Using similar parameters used in the nonadaptive simulations, the results for 5, 10, and 15 infected samples with a maximum pool size of 64 yielded an average accuracy score of 98%, 95% and 90% respectively.
With a maximum pool size of 16, population size of 500, and 5 infected samples, we varied the number of adaptive steps to determine an optimal amount of adaptive steps before running the remaining tests as a nonadaptive scheme. With varied adaptive steps with a maximum of 40 tests, the accuracy between the steps did not fluctuate significantly, where each accuracy was similar within 1%.
| Adaptive Cycles | Accuracy |
|---|---|
| 1 | 91.7% |
| 2 | 90.9% |
| 3 | 90.7% |
Degree Centrality Pooling
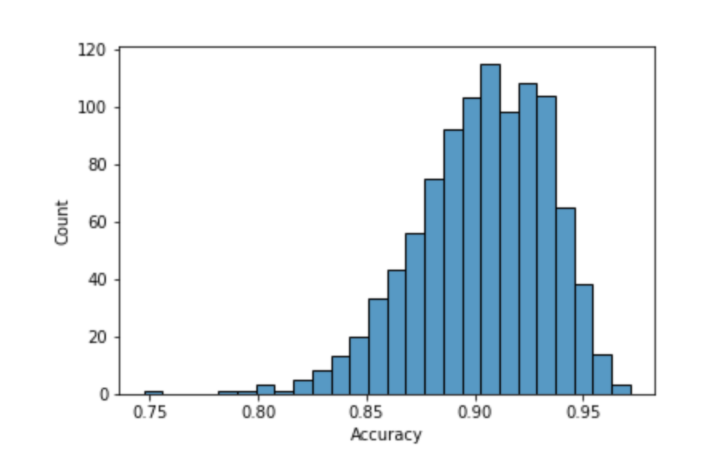
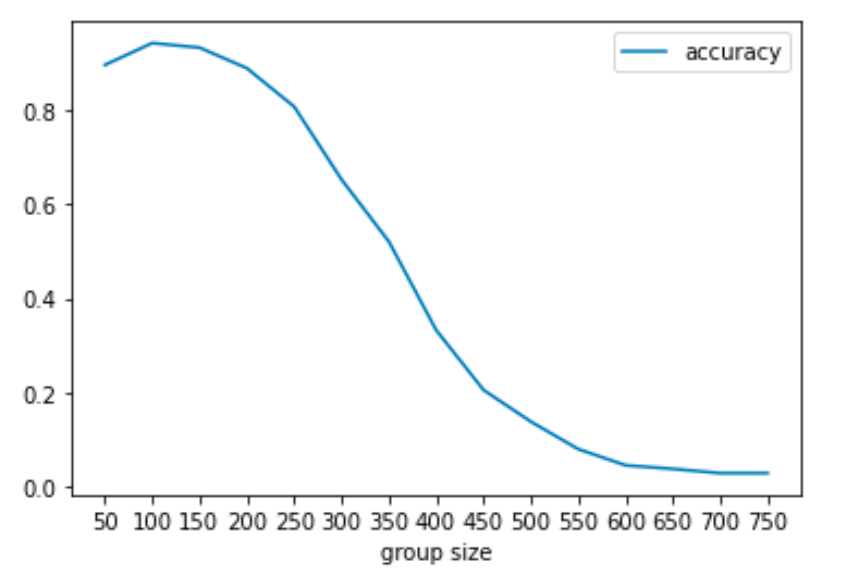
When the group size is 60, in a population with 1000 people, 20 infected people, the accuracy is around 80% for 60 tests and the accuracy still increases as group tests increases.
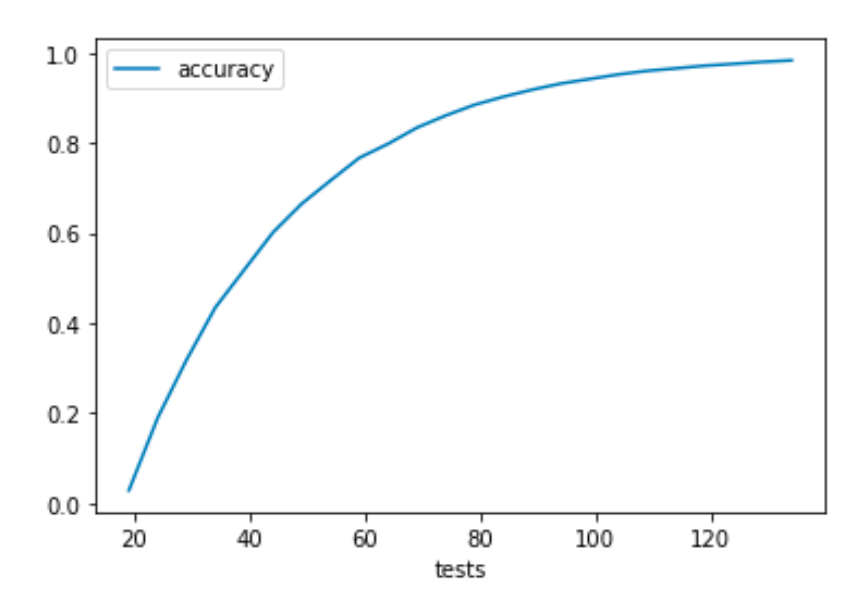
When the testing number is 65, in a population with 1000 people, 20 infected people, the accuracy reaches peak when there are about 100 people in a pool. The accuracy first increases and then decreases when pool size increases.
Tensor Based Pooling
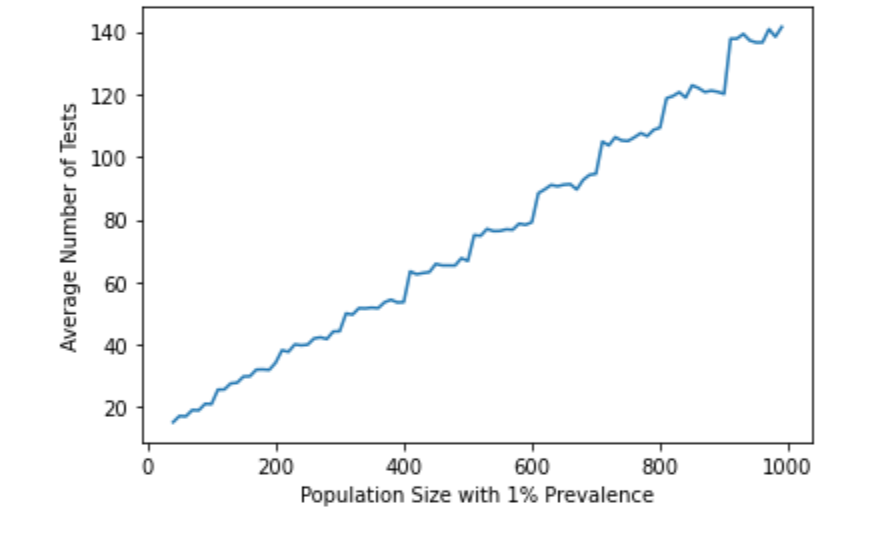
Using tensor based pooling significantly decreases the number of tests needed to find all infected samples. With a prevalence rate of 1%, running a rank 2 tensor method with additional individual sampling requires less than 20% of the original sample size.
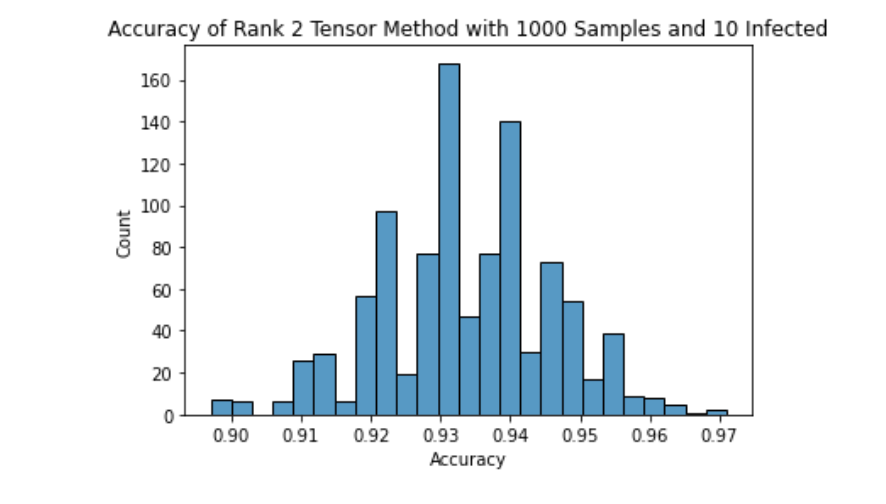
Running through simulations of the rank 2 tensor method using 1000 samples with 10 samples being infected gives an average accuracy between 93% and 94%, showing the competitiveness with Tapestry numbers.
Machine Learning Pooling
To solve the imbalance training dataset problem, we use a balanced random forest classifier to train our model. It performs bagging and bootstrapping to make the dataset more balanced and the sampling strategy is to sample only minority classes. Moreover, the class weights are applied, meaning it punishes models more harshly if it predicts positive people wrong.
The classifier returns probabilities for this node being positive and negative. We think these probabilities can be used to improve our testing accuracy. In the following pictures, it is clear to see that the difference of predictive probabilities for positive and negative people are significantly different
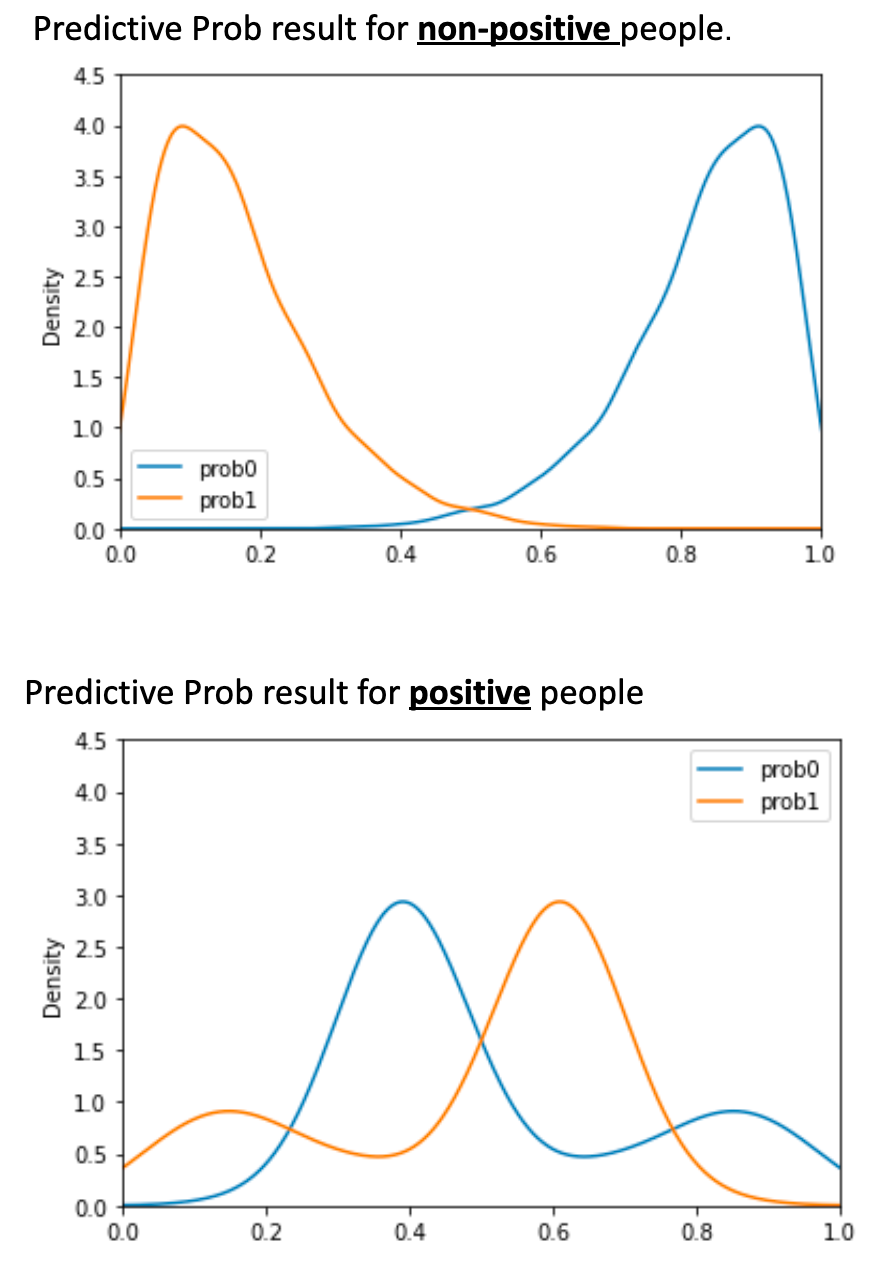
However, the trained classifier does not apply to other generated networks as different randomness is added in every other generated network. The differences of its predictive probabilities are not significant differences as it did in the last network.
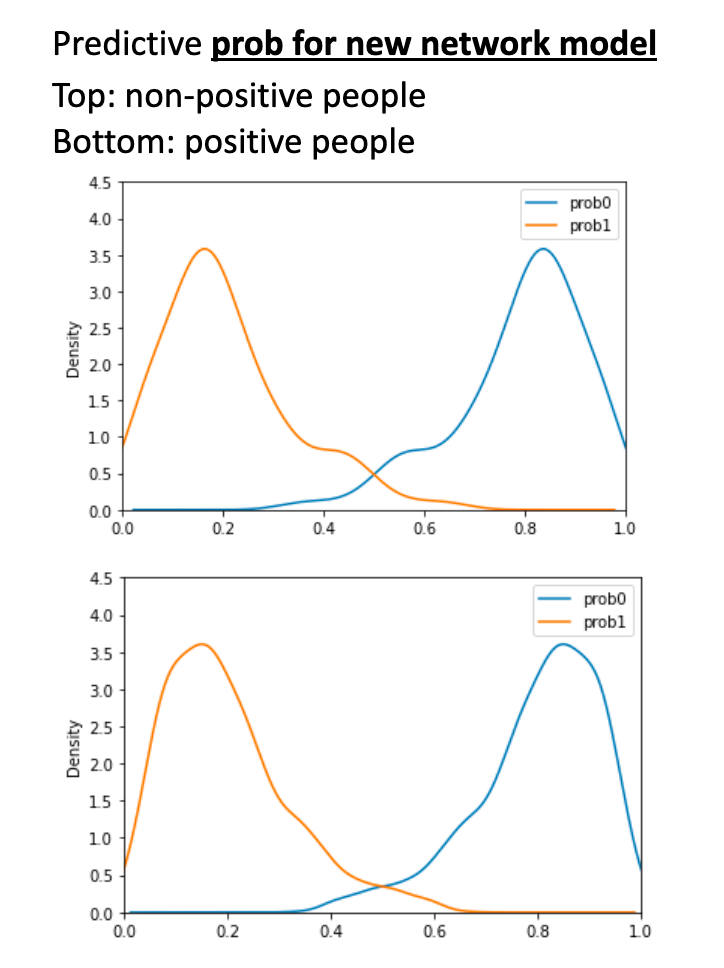
To overcome this problem, we decided to use a portion of the data to train the network to ensure the classifier applies to the testing dataset. However, it forms a dilemma: in order to do that we need to perform a large number of individual tests to get positive status for training at the beginning. We also need to do many group testing beforehand to get enough infected count features. These together cost a lot of testing. But if we do not do that, our classifier won’t be trained well and will perform poorly for the rest of the population.
Our conclusion is that we do not have enough real world data. If we do, it solves both problems list above: we do not have to perform many testings beforehand as trained data already provided; the trained classifier definitely would apply to new testing data as they all come from real world networks.